Comparing Fractions
We have moved into working on comparing fractions. There are numerous ways that we have learned to do this. Here are the ways that we have been working on:
Draw a picture. This strategy can work with smaller fractions, but starts to get complicated with larger fractions.
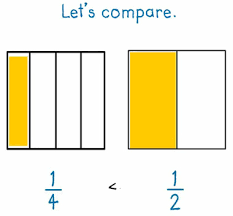
Compare with like denominators. When the denominators are the same, you are comparing the numerator. The larger numerator will be the larger fraction.











Draw a picture. This strategy can work with smaller fractions, but starts to get complicated with larger fractions.
Compare with like denominators. When the denominators are the same, you are comparing the numerator. The larger numerator will be the larger fraction.
Compare with like numerators. When the numerators are the same, you are comparing the denominator. The larger the denominator, the smaller the pieces will be. Therefore, the smaller denominator will give you the larger fraction.
Compare to a benchmark fraction. Determine how the fraction relates to ½ and that can help determine the larger or smaller fractions. We have also put them on a number line to help us clearly see how they compare.

Compare missing pieces. The fraction with the smallest piece missing will be the largest fraction.
Change one denominator to make a common denominator. Sometimes you only have to change one of the denominators to make common denominators.
Change both denominators to a common denominator. This allows kiddos to then compare fractions with like denominators. These are a few strategies we have talked about relating to this:
- Change both denominators to a common denominator.

- Multiply the denominators by each other to find a common denominator.
- Find the least common denominator. Finding the LCD has kiddos finding the least common multiple/product (the smallest positive number that is a multiple of two or more numbers).



Steps to find the LCD (Least Common Denominator)
Example: Compare 1/2, 1/3, 1/5
1. Identify the denominators.
- 2, 3, 5
2. Find the Least Common Multiples (LCM) of the three denominators. The LCM is also the Least Common Denominator (LCD).
- Multiples of 2: 2; 4; 6; 8; 10
- Multiples of 3: 3; 6; 9; 12; 15
- Multiples of 5: 5; 10; 15; 20; 25
- Note that if no common denominator exists at this point, you may need to continue writing out multiples until you eventually come across a shared multiple.
- Example: 2 x 15 = 30; 3 x 10 = 30; 5 x 6 = 30
- The LCD = 30
3. To write equivalent fractions, multiply the numerator by the same number the denominator was multiplied by to get the common denominator.
Example: 15 x (1/2); 10 x (1/3); 6 x (1/5)
New mathematical statement: 15/30 > 10/30 > 6/30
Here are some games to help solidify these skills:
Please let me know if you have any questions.


No comments:
Post a Comment